×

Cardiac marker:- Part 1 – Diagnosis of Acute Myocardial Infarction (AMI)

August 21, 2023Chemical pathologyLab Tests

Diagnosis of Acute Myocardial Infarction (AMI)

Sample for diagnosis of Acute Myocardial Infarction (AMI)

  1. The best sample is Venous blood to get a clear serum.
  2. Heparinized plasma can be used.
  3. Rapid Troponin-T can be done on whole blood (some available methods).
  4. Current recommendation on admission with the possibility of acute MI, a blood sample should be taken at intervals of:
    1. Blood sample at admission.
    2. Second sample at 2 to 4 hours.
    3. Third sample at 6 to 8 hours.
    4. Fourth sample at 12 hours.
  5. The serum can be stored at room temperature for 4 to 8 hours.
    1. At 4 °C, the serum is stable for  1 to 2 days.
    2. The serum is stable for 24 hours for troponin-T at 2 to 8 °C.

Precautions for diagnosis of  Acute Myocardial Infarction (AMI)

  1. I/M injection may raise the level of CPK.
  2. Strenuous exercise and recent surgery may raise the CPK level.
  3. Early pregnancy may decrease the CPK level.

Definition of Acute Myocardial Infarction (AMI)

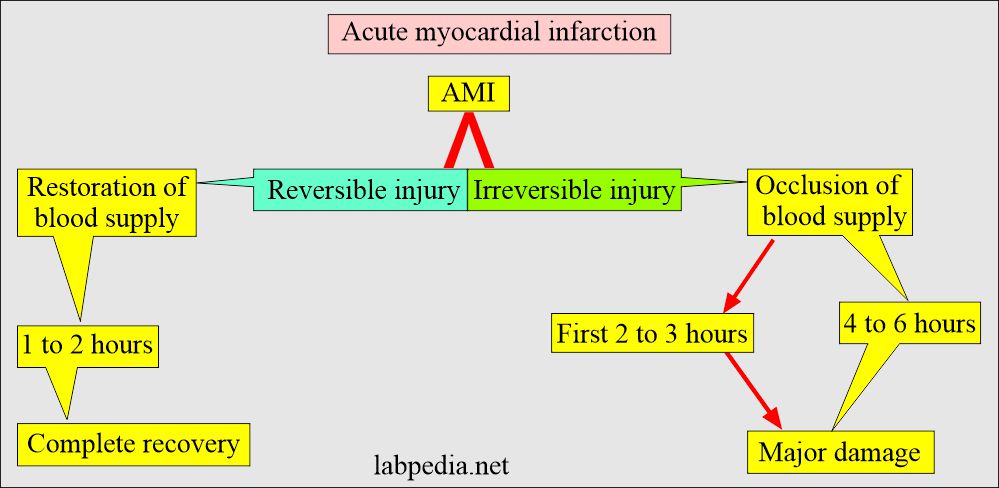
  1. This is characterized by the ischemia of the myocardial muscles. Also, this myocardial ischemia results in irreversible myocardial cell damage or death (necrosis).
    1. Or when there is obstruction of the blood supply to any part of the heart and necrosis of the muscles, or massive cell death occurs.
    2. It is almost always caused by atherosclerosis of the coronary arteries, followed by thrombosis.
    3. Clinical S/S is very important in both suspicious and diagnosed cases of AMI.
    4. Diagnosis depends upon the type of pain, its distribution, and its response to nitroglycerine.
    5. The pain characteristics are typical, and pain will respond to nitroglycerine.
    6. 20% to 30% of Acute Myocardial Infarctions (AMI) are painless.
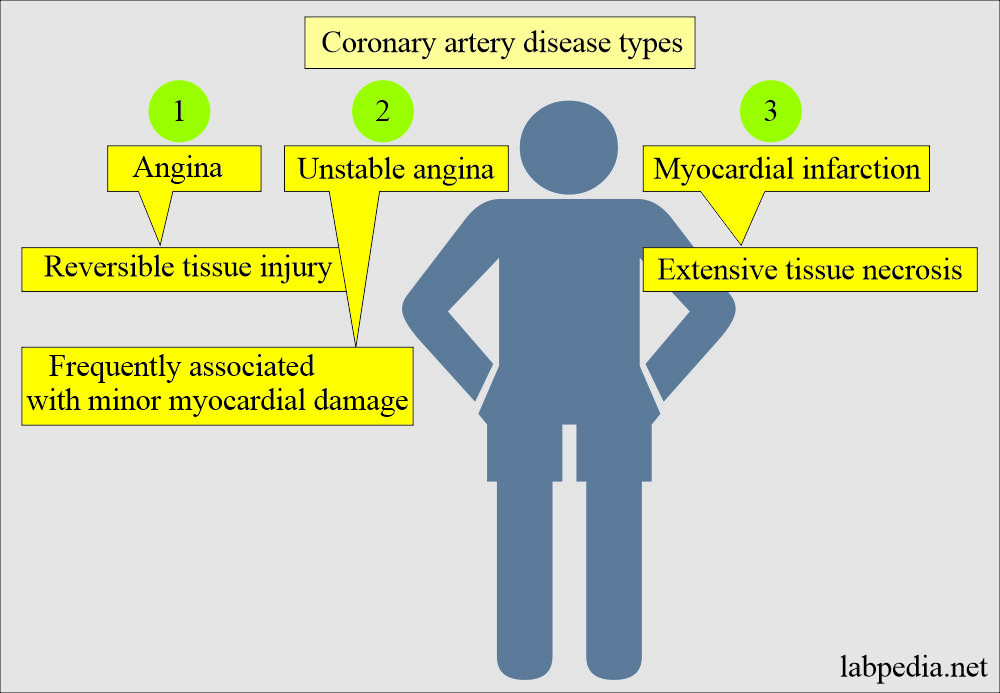
  2. Acute Coronary syndrome includes:
    1. Silent ischemia.
    2. Stable angina.
    3. Unstable angina.
    4. Non-ST wave elevation.
    5. Non-Q wave.
    6. Infarction to typical acute myocardial infarction (AMI).
Acute Myocardial Infarction (AMI): Types of ischemic heart diseases

Acute Myocardial Infarction (AMI): Types of ischemic heart diseases

Types of acute myocardial infarction (AMI):

  1. Silent myocardial infarction, where 40% to 50% of patients do not notice the typical signs and symptoms of acute myocardial infarction.
    1. These are diagnosed on the ECG.
    2. This is usually seen in diabetic patients and hypertension.
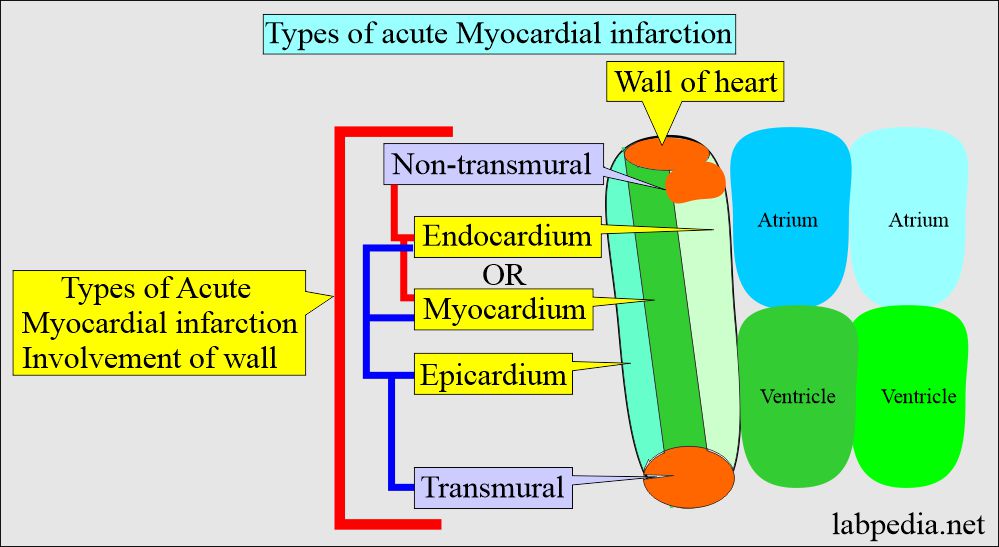
  2. The AMI is classified based on anatomic, morphologic, and diagnostic clinical data:
    1. Nontransmural AMI is when there is the involvement of only the endocardium or both endo and myocardium.
    2. Transmural MI occurs when all three endo, myo, and epicardium layers are involved.
Types of acute myocardial infarction (AMI)

Types of acute myocardial infarction (AMI)

  1. Another classification is:
    1. Non-Q wave subendocardial infarction.
    2. Q-wave was transmural infarction.

Pathophysiology of acute myocardial infarction

  1. There is an increased risk of AMI with increasing age.
    1. 4 to 5 times more risk in men between the ages of 45 to 54 years than women.
    2. The risk is the same in both sexes (men and women) after the age of 80 years.
  2. Before acute myocardial infarction occurs, there is transient ischemia where the oxygen supply is deprived of the muscle, which is called an Anginal attack.
    1. In angina, there is no necrosis.
  3. The major cause of AMI is atherosclerotic plaques and thrombus formation.
  4. Ischemia starts from the endocardium and then spreads outwards.
  5. Irreversible muscle damage occurs during ischemia for at least 15 to 20 minutes.
    1. Vasospasm and platelet aggregation may contribute to coronary occlusion.
Acute myocardial infarction out come

Acute myocardial infarction outcome

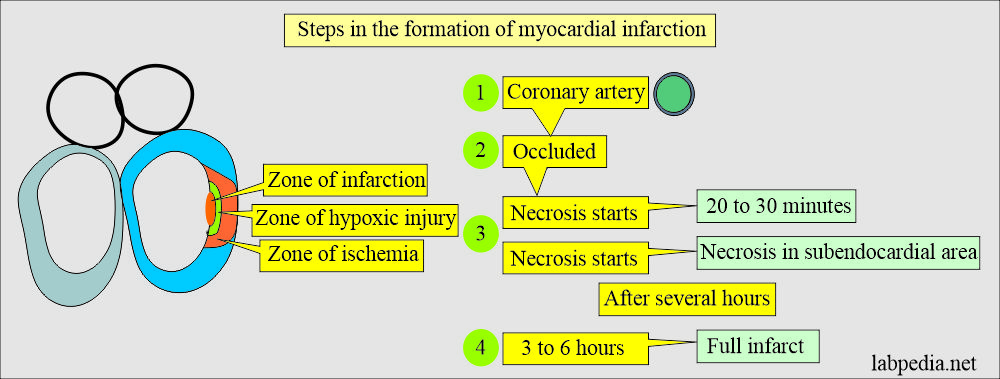
  1. Myocardial necrosis starts:
    1. The necrosis process starts in 20 to 30 minutes.
    2. Infarcts start in the subendocardial area.
    3. After several hours, a mid and subepicardial area of the myocardium is involved.
    4. After 3 to 6 hours, there is full infarct formation.
      1. Streptokinase injection can limit the infarct.
AMI stages for acute myocardial infarction

AMI stages for acute myocardial infarction

Changes in the myocardial infarction:

Time period Gross changes Microscopic changes
  • 0 to 30 minutes
  • No change seen
  1. Changes are reversible
  2. Mitochondrial swelling
  • 1 to 2 hours
  • Still no change
  • Few wavy fibers at the margin of the infarct
  • 4 to 12 hours
  • Still no change
  1. Early coagulation necrosis
  2. Minimal hemorrhage
  3. Edema
  4. Occasional polys infiltrate
  • 18 to 24 hours
  • There is slight pallor
  1. Coagulation necrosis
  2. Nuclei are pyknotic
  3. Cytoplasmic eosinophilia
  4. Polys infiltrate
  5. Necrosis at the periphery of the infarct
  • 24 to 72 hours
  • Pallor is prominent
  1. Coagulation necrosis is complete
  2. Heavy polys infiltrate
  3. Nuclear fragmentation of the polys nuclei
  • 4 to 7 days
  1. Center is pallor
  2. Surrounding hyperemic border
  3. Infract looks pale and firm
  4. Infarct is well-defined
  1. Infiltrate of macrophagic cells seen
  2. Early disintegration and phagocytosis of necrotic fibers
  3. Granulation tissue forms at the edge of an infarct
  • 10 days
  1. It is yellow in color
  2. It is soft in consistency
  3. Borders are shrunken and purple in color
  1. Phagocytosis is prominent
  2. Well-formed granulation tissue in the peripheral area of the infarct
  • 4th week
  • The Infarcted area is pale
  1. Necrotic myocardium is reabsorbed
  2. Granulation is mature
  3. Vascularity decreases
  4. Amount of collagen increases
  • 7 to 8 weeks
  • The infarcted area is firm and grey
  1. The process of fibrosis starts
  2. There is a dense scar

Distribution of the infarct:

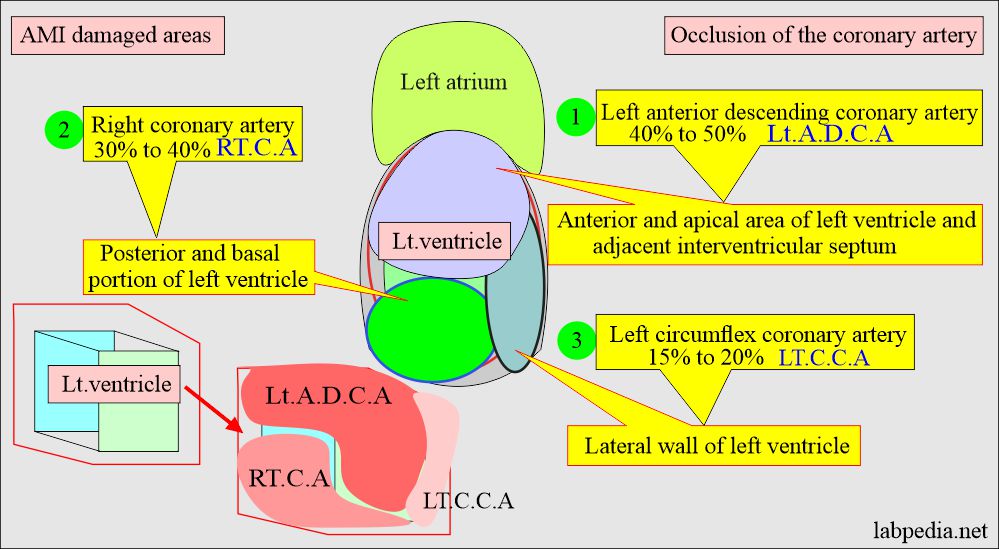
  1. The ischemic necrosis involvement of the heart muscle depends upon the involvement of the anatomical blood vessel occlusion.
    1. The anterior left descending coronary artery involves the Anterior and apical part of the left ventricle and adjacent interventricular septum.
    2. The left circumflex coronary artery involves the Lateral wall of the left ventricle.
    3. The right coronary artery involves a Posterior and basal portion of the left ventricle.
Acute myocardial infarction (AMI) showing damage to the heart wall

Acute myocardial infarction (AMI) showing damage to the heart wall

Risk factors for Acute myocardial infarction (AMI) are:

  1. Family history is a very important factor.
  2. Physical activity, including walking or exercise.
  3. Lifestyle.
  4. Hypertension.
  5. Tobacco use.
  6. Weight (obesity), diet, and nutrition.
  7. Diabetes mellitus.
  8. Hyperlipidemia.
    1. High cholesterol.
  9. Sex is more common in males.
  10. More common in the case of family history.

Signs and symptoms of Acute myocardial infarction (AMI):

  1. Chest pain in the mid-thorax, and there is crushing substernal pain.
  2. Pain may radiate to teeth, jaw, shoulder, arm, or back.
  3. There may be dyspnea or shortness of breath.
  4. There may be sweating.
  5. There may be epigastric discomfort with or without nausea and vomiting.
  6. The patient may go into syncope.
    1. In 50% of patients, the AMI is preceded by angina pectoris.
  7. The pain of AMI is not relieved by nitroglycerin.

Acute Myocardial infarction is characterized by:

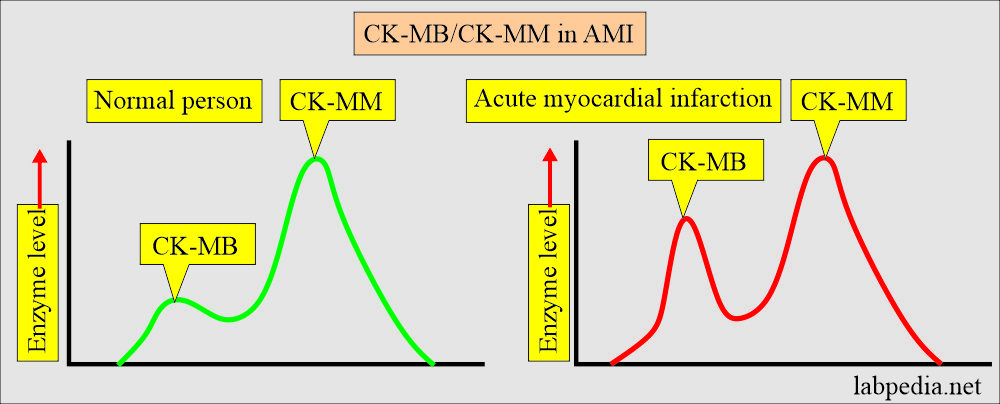
  1. The typical rise of CK-MB. The more rapid rise and fall of CK-MB.
  2. Raised level of Troponins. The more rapid rise and fall of Troponins.
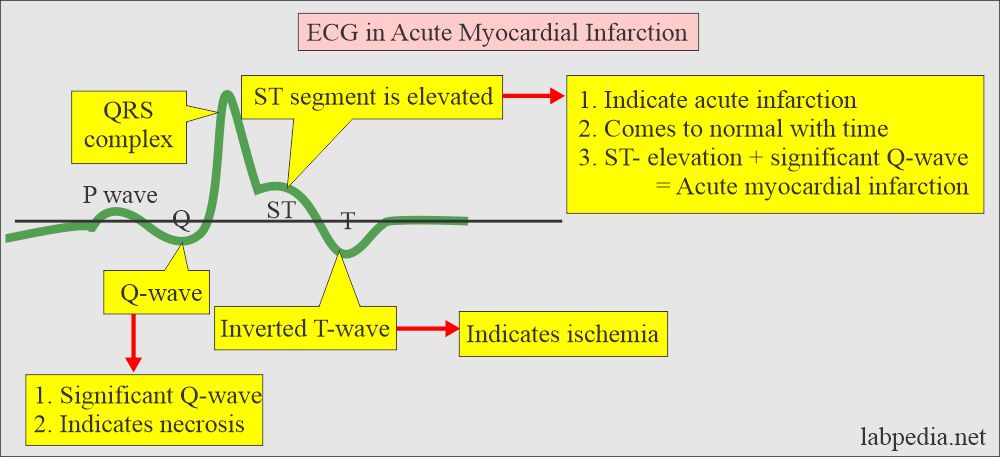
  3. ECG changes.
    1. Development of Q-wave.
    2. ST-segment elevation.
  4. A coronary angiogram shows coronary artery abnormality.
Acute myocardial infarction diagnostic criteria

Acute myocardial infarction diagnostic criteria

Diagnose of acute Myocardial infarction (AMI):

H/O chest pain:

  1. Chest pain may be typical in the case of AMI. This may be present in the left arm and may radiate to the mandible.
  2. This pain may be in the interscapular area, mimicking gallbladder pain.
  3. In some patients, there is silent AMI, which is most common in people with diabetes.
AMI chest pain and ECG changes

AMI chest pain and ECG changes

Changes in the ECG:

  1. The initial ECG is diagnostic in more than 50% of the cases.
  2. 15% of the cases show no initial changes in ECG.
  3. Follow-up for 24 hours shows positive ECG in 75% of the cases.
    1. These changes are reflected in the ST-segment, T-wave, and enlarged Q-wave.
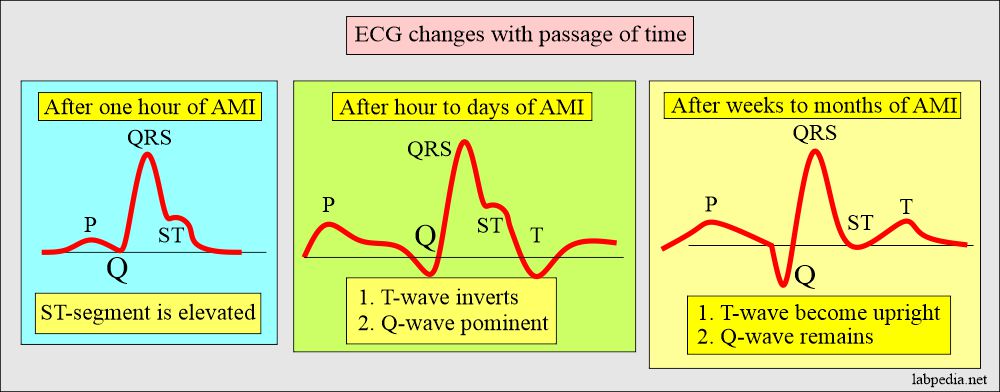
    2. Initially, there is the elevation of the ST segment.
    3. Later on, Q-wave becomes prominent.
    4. After weeks to months, the ST segment becomes normal.
    5. T-wave also comes back to its original position.
    6. But Q-wave remains abnormal.
ECG changes in acute myocardial infarction (AMI)

ECG changes in acute myocardial infarction (AMI)

ECG changes with passage of time

ECG changes with the passage of time

Abnormal cardiac enzymes:

  1. CK.
  2. CK-MB.
  3. LDH.
  4. Myoglobin.
  5. Troponin T and I.
  6. SGOT.

CK and CK-MB

  1. CK is found in the heart muscles, skeletal muscles, and brain.
  2. CK Can reflect the timing, quantity, and resolution of MI.
  3. CK has isoenzymes:
    1. CK-1 =BB = Found predominantly in the brain and lung.
    2. CK-2 =MB = Found predominantly in the cardiac muscles.
    3. CK-3 =MM = Found predominantly in the skeletal muscles.
  4. CK-MB is more specific for cardiac muscle injury.
AMI showing CK-MB and CK-MM pattern

AMI showing CK-MB and CK-MM pattern

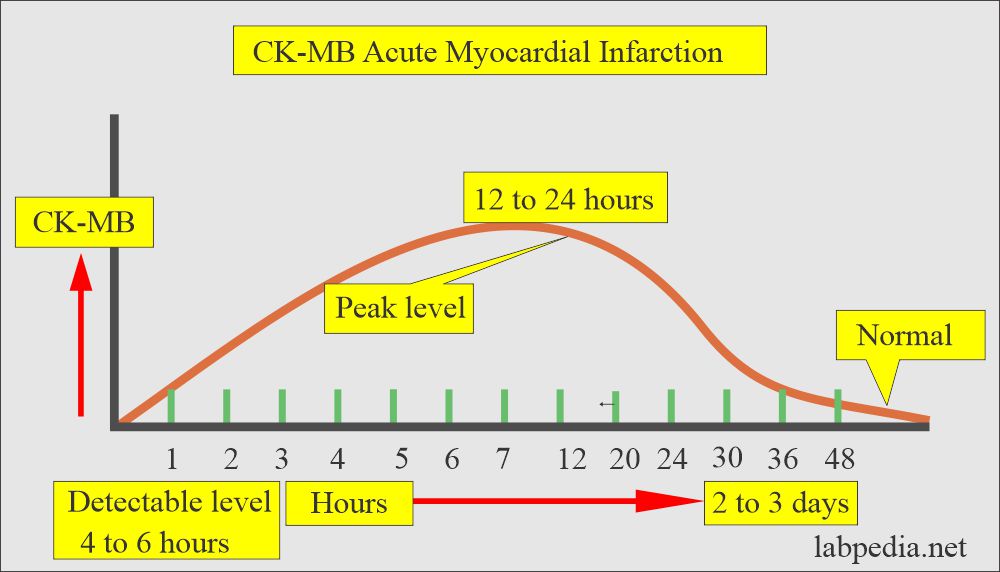
CK-MB interpretations:

  1. This also helps in quantifying and giving a degree of myocardial injury.
  2. If there is no further myocardial damage, then:
    1. CK-MB was detected in the first 3 to 6 hours.
    2. The peak level is at 20 to 24 hours.
    3. This returns to normal in 12 to 48 hours (another reference becomes normal in 72 hours).
    4. By 72 hours, 2/3 of the patients still show some increase in CK-MB.
    5. Sampling every 6 hours is more likely to find peak levels.
    6. Diagnosis of AMI is confirmed within 8 to 12 hours.
    7. Sampling beyond 24 hours is not advised.
    8. The single sample value is not diagnostic; serial estimation at least 4 hours apart shows ≥a 50% increase.
    9. Serial measurement is more important, and diagnosis reaches 100%.
  3. Total CK may be normal, but CK-MB will be raised.
  4. Raised CK-MB with normal total CK will represent patients with non-Q-wave AMI.

Disadvantages of CK-MB:

    1. A rapid return to normal makes it a poor marker.
    2. CK-MB is not as specific as Troponin, and there are false-positive reports of non-ischemic cardiac injuries like pericarditis and myocarditis.
    3. CK-MB is also positive in muscular dystrophy, exercise, and rhabdomyolysis.
  2. CK-MB usually does not arise in the case of angina, pulmonary embolism, or congestive heart failure.
    1. CK-MB may rise in case of shock, malignant hyperthermia, myopathy, or myocarditis.
  3. There is a small amount of CK-MB in the skeletal muscles.
    1. A case of severe skeletal muscle injury may give rise to a significantly high level of CK-MB.
  4. CK-MB is more helpful and more specific than Myoglobin when the patient comes with chest pain after 10 to 12 hours.

CK-MB relative index:

  1. This is done to avoid skeletal muscle injury with myocardial muscle damage.
  2. Calculation:
    1. CK-MB/total CPK
    2. Normal CK-MB/Total CPK index = <2.5.
  3. Examples:
    1. If CK-MB = 3.0 ng/mL
      1. Relative index = ≥2.5
      2. This is highly suggestive of myocardial injury.
    2. If CPK-MB = >3.0 ng/mL
      1. Relative index = <2.5
      2. Not diagnostic for myocardial injury.
Ck-MB in acute myocardial infarction (AMI)

Ck-MB in acute myocardial infarction (AMI)

Changes in Acute myocardial infarction (AMI) of lactate dehydrogenase (LDH)

Changes in Acute myocardial infarction (AMI) of lactate dehydrogenase (LDH)

  1. Rises within 24 to 48 hours of Acute MI.
  2.  The peak level is 2 to 3 days.
  3. Returns to normal in 5 to 10 days.

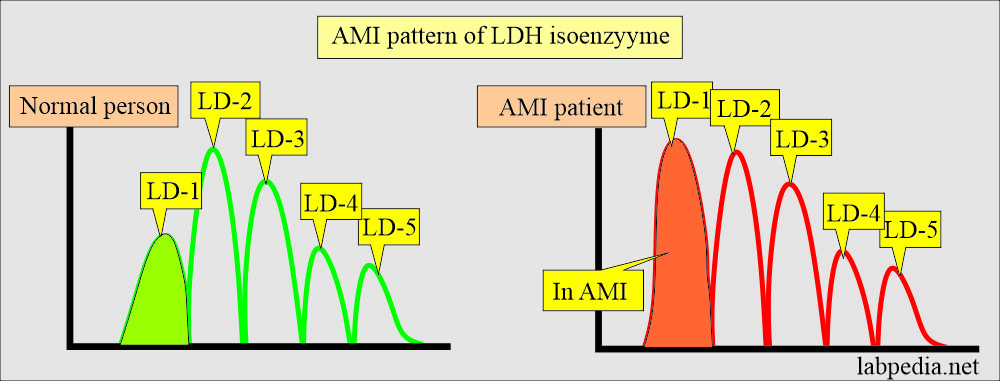
Lactate dehydrogenase (LDH):

Disadvantages of LDH:

  1. LDH has significance in other diseases like:
    1. The elevated level in the urine indicates malignancy or injury to the urinary system.
    2. LDH is also found in pleural, cardiac, or peritoneal effusions.
      1. When the effusion LDH/serum LDH ratio is >0.6, it indicates exudate in the effusion fluid.
  2. LDH is not tissue-specific because of its distribution throughout the body.
    1. It is raised in a variety of diseases, including myocardial injury.
    2.  It is also not specific to cardiac diseases.

Myoglobin:

  1. Myoglobin is an oxygen-binding protein of the skeletal and cardiac muscles.
  2. Myoglobin is most sensitive to the cardiac marker and is the earliest marker of acute myocardial infarction.
    1. But this is the least cardio-specific of cardiac markers.
  3. This is cardiac and skeletal muscle protein. This can increase after trauma to skeletal muscle or cardiac muscle injury.
    1. This is not specific to cardiac muscle injury because it will rise even with there is a minor injury to skeletal muscle.
    2. It is raised in the trauma, inflammation, or ischemic changes to skeletal muscles.
  4. But Myoglobin is very sensitive to CK and CK-MB during the first hour of chest pain.
    1. It rises in the first 1 to 4 hours and is detectable in 6 to 9 hours.
    2. The peak level is at 8 to 12 hours.
    3. It becomes normal within 24 to 36 hours.
    4. Sensitivity is >95% within 6 hours of the appearance of the symptoms.
    5. It appears before the CK-MB around 2 to 5 hours.
    6. If Myoglobin remains within the reference range 8 hours after the start of chest pain, then essentially, Acute MI can be ruled out.
  5. Myoglobin is not recommended in patients with renal failure because they will have a raised level due to decreased kidney clearance.
  6. The disadvantage of myoglobin:
    1. A myoglobin sample is taken at a 1-hour interval.
    2. There is a wide range of the normal value from 6 to 90 ng/mL.
    3. Myoglobin displays a low specificity for AMI, as this is also raised in renal diseases, shock, open-heart surgery, skeletal muscle damage, and drastic exercise.
    4. This may also be raised in muscular dystrophy.
    5. Values are usually high in uremia and muscular trauma as compared to AMI.

SGOT

  1. This was the first enzyme marker for MI but lakes cardiac specificity, so it lost its value.
  2. SGOT sometimes raised in 90% to 95% of acute AMI.
  3. It is raised and found in the first 8 to 12 hours of heart muscle necrosis (ischemia), AMI.
    1. The peak level is 24 to 48 hours after the AMI attack.
    2. It falls to normal within 3 to 8 days.
  4. The disadvantage of SGOT:
    1. SGOT level does not correlate with tissue necrosis of the heart in AMI. There may be a minimal rise in the SGOT level.
    2. This may be raised in the case of liver cells, skeletal muscles, kidneys, and pancreas parenchymal cells injury.
    3. SGOT’s main drawback in diagnosing AMI is that it may be raised in many other conditions.

Hydroxybutaric acid dehydrogenase (HBD)

  1. It is used as a substitute for LDH-1.
  2. HBD indirectly measures LDH-1 (heart) activity.
  3. HBD is easy to measure and cheaper as compared to LDH isoenzymes.
  4. Once there are elevated cardiac enzymes, they may follow with HBD.

Troponin (Tn) T

  1. The troponin protein complex is situated on the thin filament of skeletal and cardiac muscles.
    1. Troponin is highly concentrated in cardiomyocytes.
  2. The role of Troponin is calcium-mediated contraction through its action with actin and myosin.
  3. Troponin complex can be separated by the monoclonal antibodies consisting of:
    1. TnT (Troponin – T) is a tropomyosin-binding subunit.
    2. TnI (Troponin – I) is the myosin ATPase inhibiting subunit that blocks the myosin movement without calcium.
    3. TnC (Troponin – C) is the calcium-binding subunit.
  4. Cardiac troponins are separated by the immunoassay with the help of monoclonal antibodies into:
    1.  Troponin – T.
    2. Troponin – I.
  5. Troponin is localized in:
    1. Myofibrils are 94% to 97%.
    2. A cytoplasmic fraction is 3% to 6%.
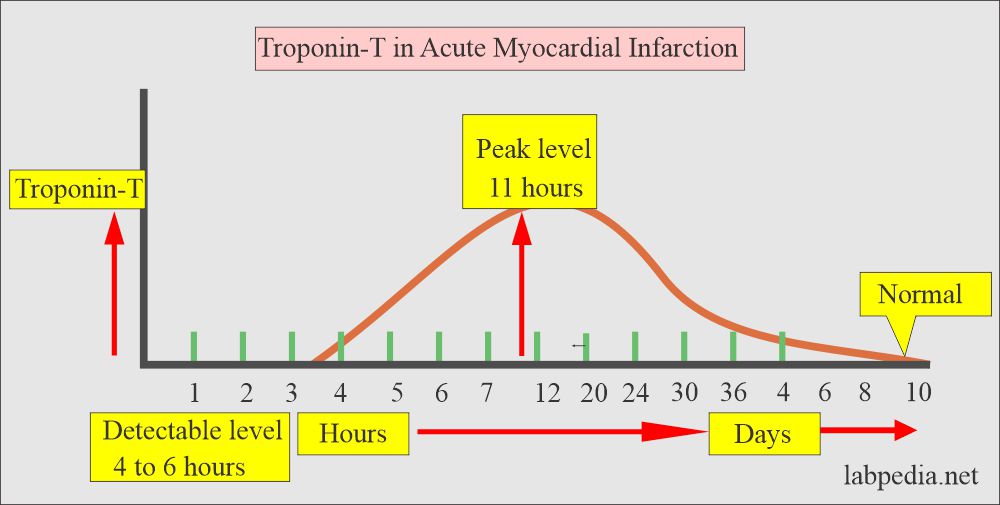
  6. Troponin -T allows the early and late diagnosis of MI.
  7. The serum level remains raised beyond 7 days.
    1. It can be detected as early as 3 hours after the myocardial injury.
    2. Troponin -T remains elevated for 10 to 14 days.
    3. Troponin-I stays elevated for 7 to 10 days.
Changes in acute myocardial infarction (AMI) of Troponin-T

Changes in acute myocardial infarction (AMI) of Troponin-T

  1. The sensitivity of Troponin – T is 100% from 12 hours to 5 days after the chest pain.
    1. The raised level is also significant because it may go even up to 200 times.
  2. Serial measurement of Troponin-T and Troponin-I is advisable and specific for diagnosing AMI (myocardial damage).
  3. Raised levels of Troponin-T in unstable angina predict poor outcomes in some patients.
  4. Troponin measurement is better than LDH, particularly in patients who seek medical attention more than 24 to 48 hours after the onset of symptoms.
  5. Troponins are measured by:
    1. Monoclonal antibody immunoassay.
    2. Enzyme-linked immunoassay.
    3. Monoclonal sandwich antibody qualitative technique.

Advantage of Troponins over CK-MB:

Characteristic features Troponins CK-MB
  • Specificity
  1. More specifically, for cardiac muscle injury.
  2. Normal in noncardiac muscle injury
  1. Increased skeletal muscle injury, brain, lung, and renal failure
  • Increased level
  1. Increased early.
  2. Remains elevated longer than CK-MB
  1. Increased in 3 to 6 hours.
  2. Peak 20 to 24 hours, and normal by 48 hours
  • Sensitivity 
  • More sensitive to cardiac muscle injury than CK-MB
  • Less sensitive to cardiac muscle injury
  • Importance 
  • More important for the evaluation of chest pain
  • Less important for the assessment of chest pain

Normal values of cardiac markers:

Source 1

  • CK-MB = 0 to 3 ng/mL
    • Or 0 to 3 µg/L

Source 2

  • Troponin T = <0.2 ng/mL
  • Troponin I = <0.3 ng/mL

Source 4

  • Troponin-T = <0.2 ng/mL
    • Or <o.2 µg/L
    • Troponin-T = >1.0 ng/mL indicates current myocardial injury.
  • Troponin-I = <0.35 ng/mL
    • Or <0.35 µg/L
  • LDH = 140 to 280 U/L
    • LDH = 300 to 800 U/L indicates myocardial infarction.
  • Myoglobin = <55 ng/mL (25 to 72 ng/mL or 1.28 to 3.67 nmol/L)
  • SGOT (AST) = Adult male = 5 to 40 U/L
    •   Slightly lower in the female.
  • HBD = Male = 150 to 300 units/100 mL (Rosalki-Wilkerson)
    • Female = 95 to 210 units/100 mL (Rosalki-Wilkerson)
      •     (55 to 125 units by Sigma)

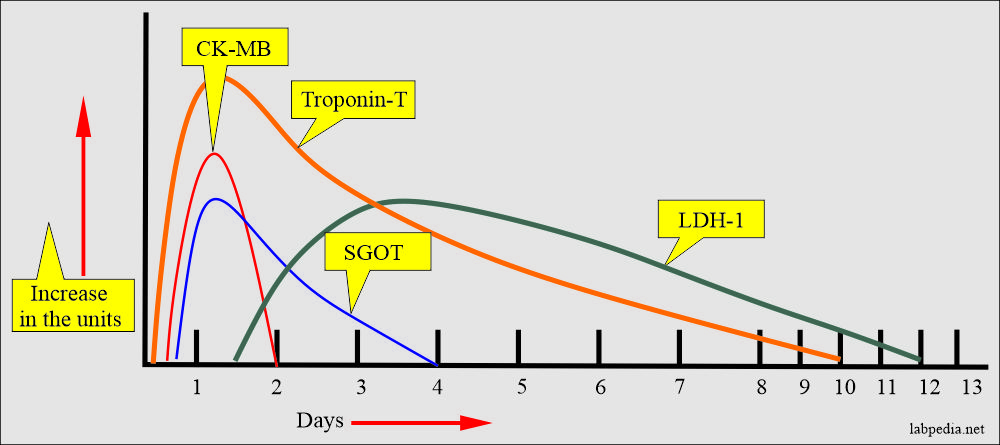
Table of cardiac markers:

Marker Time to rise in the blood (hours) When detectable in the blood (Hours) Peak  Days to become normal
Creatine Kinase 5 to 8 6 to 8 24 to 36 hours 3 to 4 days
CK -MB 5 to 15 4 to 6 12 to 24 hours 2 to 3 days
LDH 2 to 4 8 to 12 2 to 4 days 8 to 14 days
Myoglobin 1  to 3 1 to 3 6 to 9 hours 1 day
Troponin I 4 to 6 3 to 8 10  to 24 hours 3 to 10 days
Troponin T 3 to 4 3 to 8 10 to 24 hours 5 to 10 days
AST (SGOT) 3 to 5  6 to 8 24 to 48 hours 4 to 6 days
  • Thrombolytic therapy is helpful if applied within the first 12 hours of AMI.
  • Note: You may find some differences in these tests to become normal in different references.
Diagnosis of Acute Myocardial Infarction (AMI): Cardiac markers shown in the graph

Diagnosis of Acute Myocardial Infarction (AMI): Cardiac markers are shown in the graph

Critical values 

  • Troponin-I = >1.5 ng/mL (>1.6 µg/L)
  • Troponin-T = >0.1 µg/L
  • CK-MB = >5% or >10 µg/L

Questions and answers:

Question 1: Which test is more specific for AMI?
Question 2: What is the significance of myoglobin for the diagnosis of AMI?
Possible References Used
Go Back to Chemical pathology

Add Comment



The reCAPTCHA verification period has expired. Please reload the page.

Copyright © 2014 - 2025. All Rights Reserved.
Web development by Farhan Ahmad.